1、脫離點與落回點的軌跡

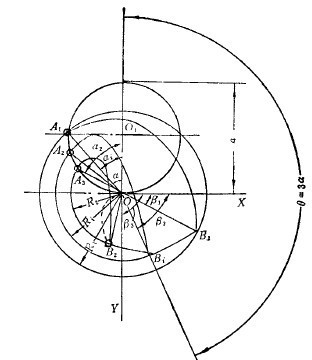
磨機中的球荷由若干層球組成，每一層球都有一個脫離點A_i和一個落回點B_i。每一層球的A_i點的坐標各不相同，但它們既然都是脫離點，就都具有相同的幾何條件。同樣，各落回點B_i的坐標盡管也不相同，但也都符合同一個幾何條件。找出這兩種幾何條件，就找出了這兩種轉折點的連線，即脫離點與落回點的軌跡。由公式可知

此處a=，當n為已給定時，a 為常數。公式（2-17）是以磨機中心O為極點，坐標軸OY為極軸的圓曲線方程，此圓的半徑為。由于每一層球皆有一脫離角a_i與球層半徑R_i，并且符合上述關系，因此諸A_i皆在以O₁為圓心及O₁O=為半徑的圓上。這個圓就是各脫離點A_i的軌跡，見圖2-8。落回點B_i到磨機中心的距離為R_i，與極軸OY之間的極角由公式可知為 點B_i也在圓運動軌跡上，它也遵從公式，于是照樣有極坐標方程式 當時，R=0，此方程式表示的曲線（即巴斯赫利螺線）將通過磨機中心（即極點）O。公式代表的曲線就是諸落回點B_i的軌跡。 

來看，以時R 的水平投影X_B為極小值。由引可見，對目前所論述的問題說，這兩個極限值只有意義，它是與小球層半徑R_小相對應的大脫離角a_大。于是，判斷球層保持明顯的圓運動和拋物線運動的極限狀態(tài)的兩個相關連的指標是

2、轉速率、裝球率和球層半徑的關系

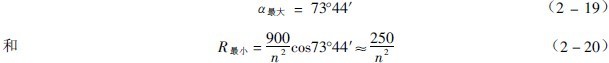
每一層球有一球層半徑和相應的脫離角，它們的關系符合公式（2-17）。設外層球的半徑為R₁，脫離角為a₁，內層球的半徑為R₂，脫離角為a₂，在磨機的每分鐘轉數為n 時，根據公式（2-17），必有下述關系

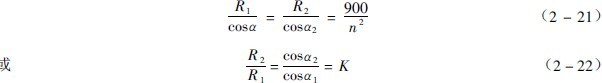
此處的K為內層球半徑與外層球半徑之比，或內層球的與外層球的脫離角的余弦之比。當外層球的半徑被看作即磨機的半徑時，它就是內層球的半徑與磨機內半徑之比。顯然，K標志裝球率，因為裝球愈多，R₂愈小，K 值也就較小。由公式可知

這兩個公式指出：外層球的脫離角僅與轉速率有關，而內層球的脫離角，即與轉速率又與裝球率（用K標志）有關。根據上面講的情況可知，為了保證內層球也能處于拋落狀態(tài)（即所有球層都是拋落的），裝球率與轉速率必有一確定關系。而且這種關系又必有臨界點，過了這種臨界點，磨機的轉速不足以使暈內層球作拋落，鋼球于是處于瀉落狀態(tài)。這里將用計算結果
繪制的曲線表示如下圖。圖中表明了裝球率、轉速率和球層半徑的關系，也表明了由這種關系所確定的瀉落和拋落的界限。

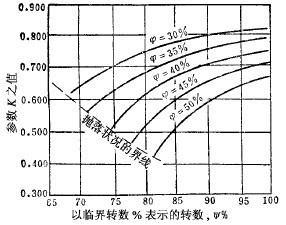
但鋼球直接打襯板會造成嚴重磨損，磨礦效果也差。磨機內的分區(qū)不僅如此明顯，而且能定量地計算出它們的范圍，下面講的球荷切面積可作說明。

3、球荷的切面積

磨機轉動時，其中有球的空間，一部分分布著作圓運動的球，另一部分分布著作拋物線落下的球。取與磨機長軸垂直的切面來看，全部運動著的球所占的面積為，而作圓運動部分的球所占的面積為₁，作拋物線運動的球所占的面積為₂，則 在動態(tài)下的裝球率為 任取一層球，它的球層半徑為R_c，脫離角為a_c，落下角為，此球層所對的圓心角為，由圖3-2-10 可以看出，  ，在R₂與R₁范圍內積分上式，得到

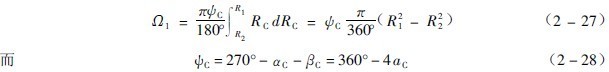
在 及₁求出之后，₂也就可以算出。例如，某磨礦機的內半徑為R，轉速率為76%，適宜的裝球率為40%，求它的球荷切面積，₁和₂。根據公式2-26，=。如果取位居中間的那層球來計算，。內層球能作拋物落下的極限條件，由公式（2-26）可知為：

此層球的落回角為 此層球所對的圓心角為：

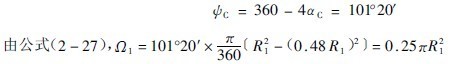
因此，在總球荷面積中，圓運動部分占62.5%，拋物線運動部分占37.5%。顯然可知，裝球太少，就很小，磨機內起磨礦作用的部分不多。裝球盡管適宜，但轉速過低，幾乎沒有₂，成為瀉落狀態(tài)，磨剝作用比沖擊作用占優(yōu)勢。只有裝球率和轉速率都適合，才能保證發(fā)生拋落狀態(tài)，并有較大的₂，使沖擊作用較為充足。